Ejercicios extras para resolver
Bibliografia
Links
-http://www.matematicasvisuales.com/html/analisis/integral/integral.html
-http://www.vitutor.com/integrales/definidas/integral_definida.html
-http://www.hiru.eus/matematicas/la-integral-definida
-http://www.fca.unl.edu.ar/Intdef/IntegralDefinida.htm
-https://www.geogebra.org/m/HzQr5MGM
PDF
-http://personales.unican.es/gonzaleof/Ciencias_2/areasC2.pdf
-http://www.uoc.edu/in3/emath/docs/Integral_Definida.pdf
-http://www.cfm.cl/~rjimenez/bioingenieria/cap4.pdf
Historia
El concepto de integral está asociado al concepto de área. Cuando una figura plana está acotada por líneas rectas es sencillo calcular su área. Sin embargo, áreas acotadas por curvas son más difíciles de calcular (incluso, de definir).
Uno de los momentos clave de la Historia de las Matemáticas fue cuando Arquímedes fue capaz de calcular el área de segmentos de una parábola usando el método de exahución de Eudoxo.
Cavalieri (alrededor de 1630) sabía como integrar funciones potencia (f(x)= x^n) desde n=1 hasta n=9. El resultado general, para n arbitrario, fue obtenido por Fermat.
Aunque Cavalieri no conocía el término 'función' podemos decir que una de sus contribuciones fue que él consideró el problema de calcular el área limitada por la gráfica de una función positiva, el eje X y dos rectas verticales (un 'trapezoide curvilíneo' o 'el área bajo una curva')
Si queremos integrar funciones lineales el problema es simple.
El problema es más difícil cuando la gráfica de la función no es una recta.
"Vamos a seguir una idea de Arquímedes. Es aproximar la función f por funciones horizontales (constantes), y el área bajo f por la suma de rectangulos pequeños." (Lang)
En estos casos queremos construir la integral definida (un número) como el resultado de algún tipo de proceso de límite. Podemos empezar dividiendo [a,b] en subintervalos y tomar la suma de las áreas de ciertos rectángulos que aproximan la función f en varios puntos del intervalo. El área de estos rectángulos aproxima la integral. La integración es un proceso de suma.
Usamos esta notación:
El símbolo S (una S alargada, por suma) se llama signo de integral y fue introducido por Leibniz en 1675. El proceso que produce el resultado se llama integración. Los números a y b, que se ponen junto al signo de integral, se llaman límite de integración inferior y superior.
Leibniz usó este símbolo porque consideraba la integral como la suma de infinitos rectángulos con altura f(x) y cuyas bases eran "infinítamente pequeñas". Fue aceptado rápidamente por muchos matemáticos porque les gustaba pensar que la integración era un tipo de "proceso de suma" que les permitía sumar infinitas cantidades "infinitesimales" (infinitamente pequeñas).
Objetivos
 Objetivo General:
Objetivo General:
-Enseñar a los estudiantes las integrales definidas mediante un blog interactivo para reforzar el conocimiento y aprender de una forma fácil.Objetivos específicos:
-Promover el intercambio de información de estudiantes así por medio del blog tenga un espacio de opinión.-Mostrar a los estudiantes las integrales definidas y su aplicabilidad en la vida diaria.
-Colaborar junto con los estudiantes y visitantes del blog para la mejora de el haciéndolo mas completo e interactivo para las personas interesadas en aprender.
Ejercicios Integrales definidas
Integral definida
- Si en cualquier figura
delimitada por rectas y por una curva; se inscriben y circunscriben
rectángulos en número arbitrario, y si la anchura de tales
rectángulos se va disminuyendo a la par que se aumenta su número hasta el
infinito, afirmo que las razones entre las figuras inscrita y
circunscrita y la figura curvilínea acabarán siendo razones de igualdad
Isaac Newton.
- El área, es
un concepto familiar para todos nosotros, por el estudio de figuras
geométricas sencillas como el triángulo, el cuadrado, el círculo y el
rectángulo. La idea o el concepto que manejamos de área, es la magnitud
que mide de algún modo el tamaño de una región acotada, es decir,
cuanto mide una superficie. Ciertamente,
para hallar el área de las figuras geométricas sencillas que ya conocemos, disponemos de fórmulas matemáticas
que facilitan este cálculo.
- Ahora, nuestro
problema consiste en encontrar un método, que nos permita calcular el área
de cualquier región, sin importar la forma que esta tenga. Para
lograr esto, es necesario primero introducir el símbolo o la notación de
Sumatoria. Para representar esto, se una la letra griega mayúscula ´sigmaµ, para abreviar
la sumatoria, y se usa de este modo:
- Si en cualquier figura
delimitada por rectas y por una curva; se inscriben y circunscriben
rectángulos en número arbitrario, y si la anchura de tales
rectángulos se va disminuyendo a la par que se aumenta su número hasta el
infinito, afirmo que las razones entre las figuras inscrita y
circunscrita y la figura curvilínea acabarán siendo razones de igualdad
Isaac Newton.
Concepto de integral definida
Propiedades de la integral definida
- Toda integral extendida a un intervalo de un solo punto, [a, a], es igual a cero.
- Cuando la función f (x) es mayor que cero, su integral es positiva; si la función es menor que cero, su integral es negativa.
- La integral de una suma de funciones es igual a la suma de sus integrales tomadas por separado.
- La integral del producto de una
constante por una función es igual a la constante por la integral de la función
(es decir, se puede «sacar» la constante de la integral).
- Al permutar los límites de una integral, ésta cambia de signo.
- Dados tres puntos tales que a < b < c, entonces se cumple que (integración a trozos):
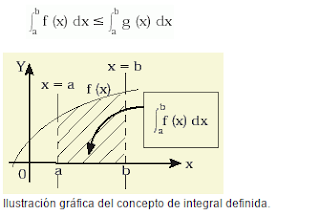
- Para todo punto x del intervalo [a,b] al que se aplican dos funciones f (x) y g (x) tales que f (x) £ g (x), se verifica que:
Introducción a las integrales definidias
- Uno de los primeros logros del cálculo, fue predecir la posición futura de un objeto, a partir de una ubicación conocida y la función que representa su velocidad. Además hemos podido, en muchas ocasiones encontrado una función a partir de valores conocidos y una fórmula para su razón de cambio. En nuestros días, calcular la rapidez que necesita un corchete en cierto punto para poder salir del campo gravitacional de la Tierra o predecir el tiempo de vida útil de un objeto a partir de su nivel de actividad y su razón de decrecimiento, son procesos rutinarios, gracias al cálculo, mediante el uso de las derivadas.
- De aquí, podemos concluir que el problema de esta es, que si conocemos el recorrido de un punto móvil, podemos calcular su velocidad y adicional mente si tenemos una curva podemos hallar la pendiente de la recta tangente en cada uno de sus puntos.Encontrar una función f a partir de su derivada, involucra el hecho de encontrar toda una familia de funciones cuya derivada puede ser f;estas funciones reciben el nombre de antiderivadas, puesto que para encontrarlas es necesario llevar el proceso contrario al de la derivación